
But 10.2 is fully below the lower outer fence, so 10.2 would be an extreme value. Since 16.4 is right on the upper outer fence, this would be considered to be only an outlier, not an extreme value. Then the outliers will be the numbers that are between one and two steps from the hinges, and extreme value will be the numbers that are more than two steps from the hinges. These values approximate, but in general do not match, the 25th and 75th percentiles reported by SPSS. SPSS follows his definition of the plot, where the upper and lower limits of the box are the Tukey hinges H1 and H2.
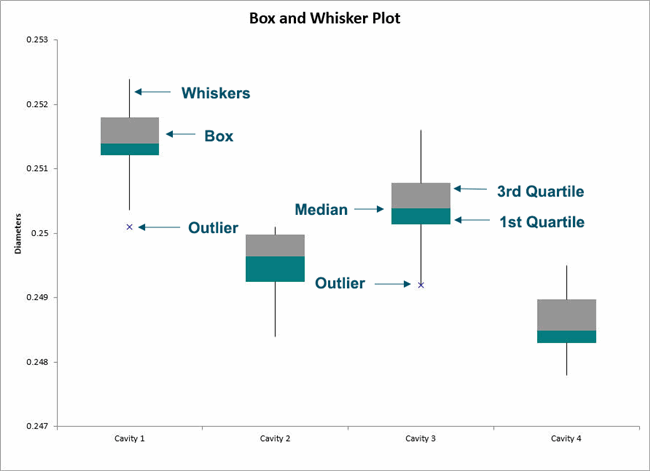
It means that the data can be divided into three quartiles. It is a special type of graph that shows the three quartiles, such as Q1, Q2, and Q3. MD Post Graduate Student at University College of Medical Sciences & GTB hospital, Delhi. In statistics, a box and whisker plot is used to display the graphical portrayal of the given set of data. It is also called as Five Number Summary box as it consists of the median, the quartiles (lower and upper) and smallest and greatest values in distribution. The outliers (marked with asterisks or open dots) are between the inner and outer fences, and the extreme values (marked with whichever symbol you didn't use for the outliers) are outside the outer fences.īy the way, your book may refer to the value of " 1.5×IQR " as being a "step". The boxplot was developed by John Tukey and presented in his book Exploratory Data Analysis. Box and whisker plot is a statistical measure to show the distribution of data. Range HIGHEST VALUE LOWEST VALUE For example, we can have the heights of a group of 8 people.
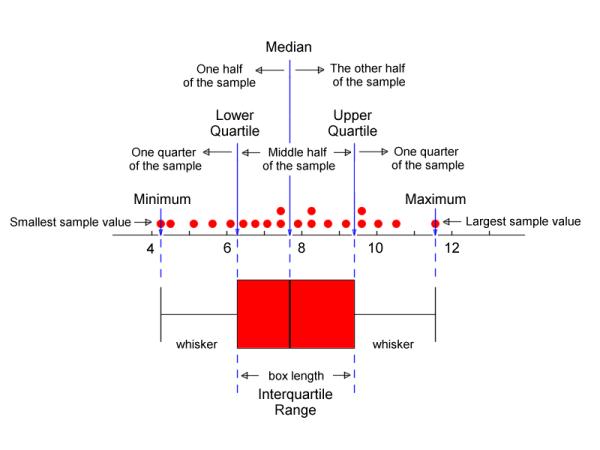
So its a measure of how big a set of values range, from lowest to highest. If your assignment is having you consider not only outliers but also "extreme values", then the values for Q 1 – 1.5×IQR and Q 3 + 1.5×IQR are the "inner" fences and the values for Q 1 – 3×IQR and Q 3 + 3×IQR are the "outer" fences. Quartiles Interquartile Range Construct Box and Whisker Plot Range The Range of a set of values, is the highest value, minus the lowest value in the set. The values for Q 1 – 1.5×IQR and Q 3 + 1.5×IQR are the "fences" that mark off the "reasonable" values from the outlier values.


 0 kommentar(er)
0 kommentar(er)
